"Ask Marilyn" Boat Problem and Solution
Problem:
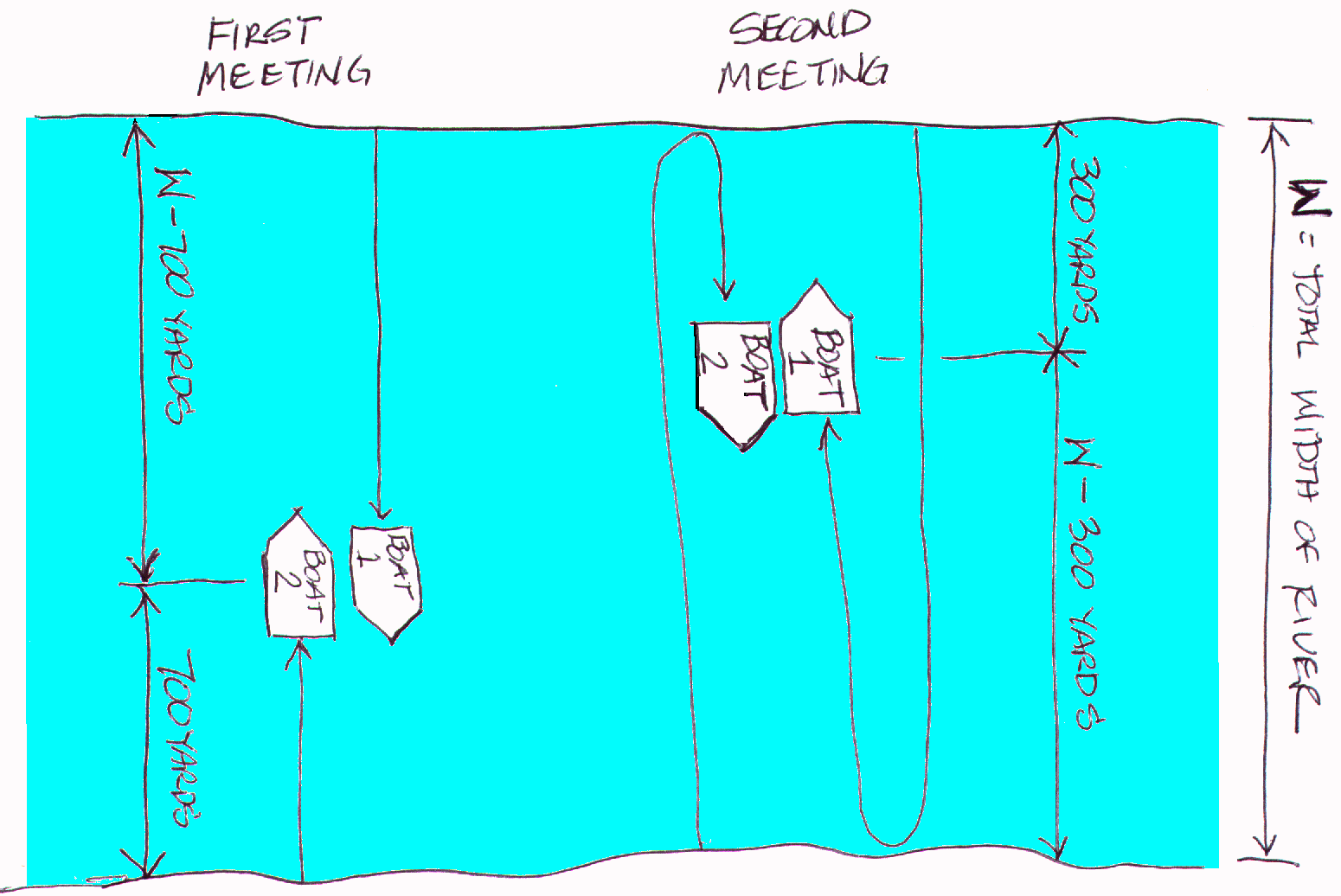
Two motorboats are on opposite shores of a river and start moving toward each other, but at different speeds. When the boats pass each other the first time, they are 700 yards from one shoreline. They continue to the opposite shores, turn around and then cross paths again at 300 yards from the other shoreline. Neglecting all other factors, like acceleration, turn-around time and current, find the width of the river.
Solution:
First, we'll draw a diagram of the situation at the two times. Note the distances from the shores. 
Next, we recognize that the basic formula we will be using is: RATE x TIME = DISTANCE
1.) Determine the relative rates of the boats from the first time they cross each other. Applying the above formula to each boat and solving for the time in each case yields:
|
Boat 1 |
Boat 2 |
Where: |
|
R 1 * t = W-700t = (W-700) / R 1 |
R 2 * t = 700t = 700 / R 2 |
R 1 = Rate of Boat 1R 2 = Rate of Boat 2W = Width of the River t = The time it took for them to meet each other the first time |
Since both boats traveled the same duration of time, we can set the right halves of the above equations equal to each other and find the rate of the first boat in terms of the rate of the second boat.
(W-700)/R
1 = 700/R2, by cross multiplication we obtain:700R
1 = (W-700)R2, then by dividing both sides by 700 we obtain R1 = (W-700)R2/7002. Now using the same formula for the relationship between rate, time and distance, we consider the entire trip of both boats.
Boat 1: Total distance traveled = W + (W-300) = 2W-300 yards
Boat 2: Total distance traveled = W+300 yards
Using a table to organize our equation setup we obtain:
|
Rate X Time = Distance |
||
|
(W-700)R 2/700 |
T |
2W-300 |
|
R 2 |
T |
W+300 |
Note that "T" = Duration of Time from when the boats first started until they crossed the second time
Multiplying across we obtain (W-700)*R2*T / 700=2W-300 as the first equation and R2*T=W+300 as the second equation. It appears that we have three variables and only two equations, however, we will see that the R2 will algebraically drop out.
Solving each for T, so we can set them equal to each other, we obtain:
Equation 1: T = (2W-300)(700) / (W-700)*R2
Equation 2: T = (W+300) / R
2Setting the right half of these equations equal to each other, we obtain:
|
(2W-300)(700) / (W-700)*R2 = (W+300)/R2 (2W-300)(700) = (W-+300)(W-700) 1400W-2100 = W*W - 400W -2100 0 = W*W - 1800W 0 = W(W-1800) W = 0 or W-1800 = 0 W = 1800 Yards |
Now multiply both sides by (W-700)*R 2Next distribute Now subtract 1400W-2100 from each side Next we factor Set each factor equal to zero Since the width cannot be zero, we throw out the left solution and solve the right one The solution |
| Opening Page |
| Christian Education |
| Networking & the Internet |
| My Background |
| Hobbies & Interests |
| Links Page |
| Email Me |